













Estude fácil! Tem muito documento disponível na Docsity

Ganhe pontos ajudando outros esrudantes ou compre um plano Premium


Prepare-se para as provas
Estude fácil! Tem muito documento disponível na Docsity
Prepare-se para as provas com trabalhos de outros alunos como você, aqui na Docsity
Os melhores documentos à venda: Trabalhos de alunos formados
Prepare-se com as videoaulas e exercícios resolvidos criados a partir da grade da sua Universidade
Responda perguntas de provas passadas e avalie sua preparação.

Ganhe pontos para baixar
Ganhe pontos ajudando outros esrudantes ou compre um plano Premium
Comunidade
Peça ajuda à comunidade e tire suas dúvidas relacionadas ao estudo
Descubra as melhores universidades em seu país de acordo com os usuários da Docsity
Guias grátis
Baixe gratuitamente nossos guias de estudo, métodos para diminuir a ansiedade, dicas de TCC preparadas pelos professores da Docsity
Um projeto de um controlador para um sistema, utilizando o método do lugar geométrico das raízes. O projeto aborda conceitos de controle automático, como controladores proporcionais, integrais e derivativos, e aplica o software matlab para a análise e simulação do sistema. Útil para estudantes de engenharia eletrónica que desejam aprofundar seus conhecimentos em controle automático e aplicar os conceitos em projetos práticos.
Tipologia: Exercícios
1 / 20

Esta página não é visível na pré-visualização
Não perca as partes importantes!













Discentes: Docentes:
Manhique, Valter Rui Eng º A. Zimbico
Maraca, Hélio José Eng º. Aristides
Maputo, Maio de 202 3
Controle: É a acção de fazer com que um sistema físico atenda as especificações de
desempenho determinadas a priori.
Controlador: Dispositivo utilizado para a obtenção do controle de um sistema físico.
Sistema de controle: Conjunto formado pelo sistema a ser controlado e o controlador.
4.2.1. Controladores em série
Consiste em colocar o controlador no ramo direto de alimentação, ou seja, em série com a
planta.
Fig.1: Controlador série
4.2.2. Controladores por realimentação
O compensador é inserido num ramo de realimentação.
Fig.2: Controlador p/ realimentação
O controlador também pode ser definido como o elemento no sistema de controle em malha
fechada que tem como entrada o sinal de erro e gera uma saída que torna a entrada. A relação entre
a saída e a entrada do controlador é frequentemente chamada
lei de controle.
Existem três formas dessa lei:
4.3.1. Controlador Proporcional (P)
O controlador P é um tipo de controlador que actua na variável controlada de forma
proporcional ao erro (como o nome sugere). Isto é, se o erro é pequeno, ele actua pouco na variável
controlada e, se o erro é grande, ele actua muito.
Fig.3: Controlador proporcional 1
u (t) = Ke(t) ⟶ U(s) = KPE(s)
Onde: e (t) = r (t) - y (t)
Para entrada degrau unitário temos que o erro é dado por: Ess=
1
1 +𝑘
O erro em estado estacionário será nulo somente para K → ∞, o que nem sempre é possível.
de erro;
sistema e dependendo das características da planta de controlo;
aumenta as oscilações, aumenta o sobressinal (MP) e reduz a estabilidade
relativa. Portanto é necessário verificar se há algum ponto de operação que
atenda a todas as exigências de controlo. Caso não atenda, deve-se usar outro
tipo de controlado.
4.3.2. Controlador Proporcional+Integral (PI)
Este tipo de controlador apresenta duas ações de controlo, nomeadamente a ação
proporcional e a ação integrativa. Apresentam, em suas ações de controlo, diferentes
proporcionalidades em relação ao sinal, de modo que, no primeiro, o sinal que sai do controlador
e vai para o sistema é proporcional ao erro, de maneira instantânea. Enquanto no segundo este
mesmo sinal é proporcional à integral do erro.
A acção de controle de um controlador proporcional-integral é definida por:
U(t) = 𝐾
𝑝
e(t) +
𝐾 𝑝
𝑇
𝑖
∫ 𝑒(𝑡)
𝑡
0
𝑑𝑡
ou, então, a função de transferência do controlador é:
𝑈(𝑠)
𝐸(𝑠)
𝑝
1
𝑇
𝑖
𝑆
) ; onde 𝑇
𝑖
é chamado tempo integrativo.
4.3.3.1. Passos para o projeto de controladores PD
dominantes de malha fechada;
satisfatório, tentar um ajuste fino dos parâmetros do controlador (Kc e z).
4.3.4. Controlador Proporcional+Integral+Derivativo (PID)
É uma técnica de controlo de processos que une as acções derivativa, integral e
proporcional, fazendo assim com que o sinal de erro seja minimizado pela acção proporcional,
zerado pela acção integral e obtido com uma velocidade antecipada pela acção derivativa.
A acção de controle de um PID é dada por:
U(t) = 𝐾
𝑝
e(t) +
𝐾
𝑝
𝑇 𝑖
∫
𝑒(𝑡)
𝑡
0
𝑑𝑡 + 𝐾
𝑝
𝑇
𝑑
𝑒(𝑡)
𝑑𝑡
e a função de transferência é:
𝑈(𝑠)
𝐸(𝑠)
𝑝
1
𝑇
𝑖
𝑆
𝑑
s)
4.3.4.1. Passos para o projeto de controladores PID
pólos dominantes de malha fechada;
de ângulo seja satisfeita;
não seja satisfatório, tentar um ajuste fino dos parâmetros do controlador (Kc, z1 e z2).
O domínio relativo dos polos de malha fechada é determinado pela relação das partes reais dos
polos de malha fechada, bem como pelo valor dos resíduos calculados nos polos. As magnitudes
dos resíduos dependem tanto dos polos como dos zeros de malha fechada.
Se as relações das partes reais forem maiores que 5 e não houver zeros nas proximidades,
então os polos de malha fechada mais próximos do eixo j ~ serão dominantes no comportamento
da resposta transitória porque correspondem aos termos da resposta transitória que decrescem
lentamente. Os polos que têm efeitos dominantes no comportamento da resposta transitória são
chamados polos dominantes de malha fechada. Muito frequentemente, os polos dominantes
apresentam-se sob a forma de um par complexo conjugado. Os polos dominantes de malha
fechada são os de maior importância entre todos os polos de malha fechada.
Note que o ganho de um sistema de ordem superior é frequentemente ajustado para ter um
par de polos complexos conjugados dominantes de malha fechada. A presença desses polos em
um sistema estável reduz o efeito de certas não linearidades, como zona morta, folga e atrito
de Coulomb.
A estabilidade de um sistema linear de malha fechada pode ser determinada a partir da localização
dos polos de malha fechada no plano s. Se qualquer um desses polos estiver no semiplano direito
do plano s , então, com o decorrer do tempo, eles darão origem ao modo dominante e a resposta
transitória aumentará monotonamente ou oscilará com amplitude crescente. Isso representa um
sistema instável.
Assim que for ligada, a saída desse sistema poderá aumentar com o tempo. Se não for alcançado
um ponto de saturação do sistema ou se não houver um fim de curso mecânico, então o sistema
poderá estar sujeito a danos e apresentar falhas, já que a resposta de um sistema físico real não
pode aumentar indefinidamente. Por isso, nos usuais sistemas lineares de controle, não são
permitidos polos de malha fechada no semiplano direito do plano s. Se todos os polos de malha
fechada se situarem à esquerda do eixo j 𝜔, qualquer resposta transitória poderá alcançar o
equilíbrio. Isso caracteriza um sistema estável.
A estabilidade ou a instabilidade de um sistema linear é propriedade do próprio sistema e
não depende da entrada ou da função de excitação do sistema. Os polos da entrada ou da função
de excitação não afetam a estabilidade do sistema, mas contribuem somente para os termos da
resposta de regime permanente na solução.
A característica básica da resposta transitória de um sistema de malha fechada está
intimamente relacionada à localização dos polos de malha fechada. Se o ganho de malha do sistema
for variável, então a localização dos polos de malha fechada dependerá do valor do ganho de malha
escolhido. É importante, então, que o projetista saiba como os polos de malha fechada se movem
no plano s , à medida que o ganho de malha varia.
Utilizando o método do lugar das raízes, o projetista pode prever quais os efeitos da variação
do valor do ganho ou da adição de polos de malha aberta e/ou zeros de malha aberta sobre a
localização dos polos de malha fechada.
Considere um sistema de malha fechada com a função de transferência seguinte:
Fig.7. Sistema de malha fechada
A equação característica desse sistema de malha fechada é obtida igualando a zero o
denominador do lado direito da equação. Ou seja, 1 + 𝐺
Aqui, vamos supor que G ( s ) H ( s ) seja uma relação dos polinômios em s. Como G ( s ) H ( s )
é uma grandeza complexa, a Equação b pode ser dividida em duas equações equiparando-se
os ângulos e módulos de ambos os lados, respectivamente, obtendo-se:
Condição angular : (c)
Condição de módulo: | 𝐺(𝑠)𝐻(𝑠)| (d)
Os valores de s que satisfazem tanto a condição angular como a de módulo são as raízes da equação
característica, ou os polos de malha fechada. Um lugar dos pontos no plano complexo que satisfaz
somente a condição angular é o lugar das raízes. As raízes da equação característica (os polos de
malha fechada) que correspondem a dado valor do ganho podem ser determinadas pela condição
de módulo.
Fig.8. Exercício
Polos dominantes em: s= - 10 ±10j
Uma vez que s= 𝜎 ± 𝜔 𝑑
→ s =- ζ𝜔
𝑛
𝑛
√ 1 − ζ
2
Sendo assim: ω
𝑑
=10 e 𝜎 = 10
Com ζ𝑤
𝑛
podemos obter o tempo de subida que é dado por:
𝑠
4
ζ𝑤
𝑛
; sendo assim 𝑡
𝑠
4
10
= 0.4s
Como ω 𝑑
=10, podemos obter ζ e 𝑤
𝑛
𝑛
10
ζ
; substituindo na formula do ω
𝑑
obtemos
10
ζ
√ 1 − ζ
2
→ ζ = √ 1 − ζ
2
→ ζ
2
= 1 - ζ
2
→ 2 ζ
2
= 1 → ζ = √ 0. 5 e, por fim, obtemos
ζ = 0.707; sendo assim 𝑤 𝑛
10
G(s) =
100
𝑠(𝑠
2
; H(s) = 1
Considerando U(s) = 0 e Gc = K, obtemos a seguinte função de transferência:
2
2
2
Equação característica: 𝑠
2
Polos: os polos são achados igualando o denominador de G(s) a zero.
2
1
=0 e 𝑆
2 / 3
= - 5 ±j8,66 ; totalizando 3 polos
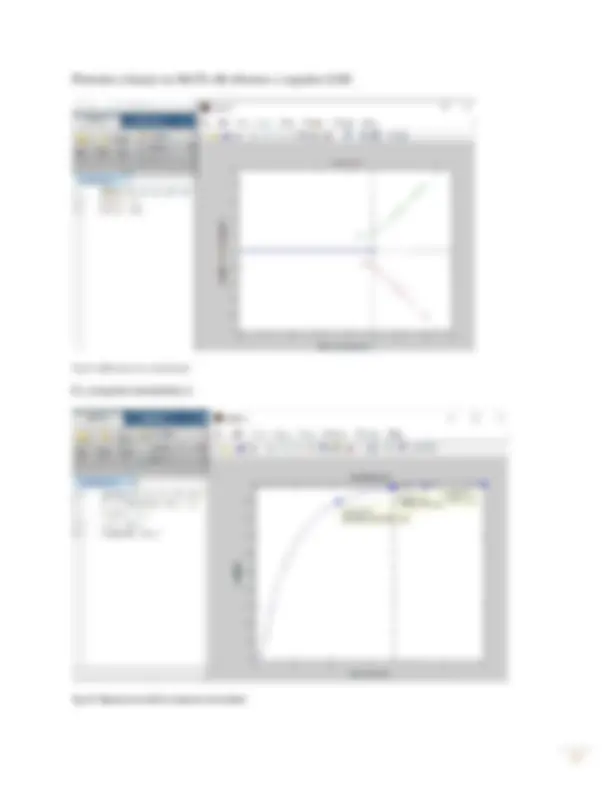
Plotando a função no MATLAB obtemos o seguinte LGR:
Fig.9. LGR antes do controlador
E a resposta transitória é:
Fig.10. Reposta transitória antes do controlador
Uma vez que os controladores PID são os mais ideais para definir polos de malha fechada,
vamos primeiro achar um controlador PID.
Gc =
𝐾𝑐
( 𝑆+𝑍 1
) +(𝑠+𝑍 2
)
𝑆
; Considerando 𝑍
1
2
= 𝑍, Gc =
𝐾𝑐(𝑆+𝑍)
2
𝑆
e G(s) =
100
𝑠(𝑠
2
; então GH(s)=
100 𝐾𝑐(𝑠+𝑧)
2
𝑆
2
(𝑆
2
Condição de fase
− 10 + 10 𝑗
100 𝐾𝐶(𝑠+𝑧)
2
𝑆
2
(𝑆
2
− 10 + 10 𝑗
− 10 + 10 𝑗
− 10 + 10 𝑗
2
− 10 + 10 𝑗
2
2 tan
− 1
10
𝑧− 10
) − 2 tan
− 1
10
− 10
2 tan
− 1
10
𝑧− 10
) − 2 tan
− 1
10
− 10
) − tan
− 1
− 100
0
2 tan
− 1
10
𝑧− 10
2 tan
− 1
10
𝑧− 10
2 tan
− 1
10
𝑧− 10
tan
− 1
tan (tan
− 1
)) = tan 180
10 = 0 (Impossível)
Como para um controlador PID o valor de z é indefinido, vamos tentar um controlador diferente.
tan
− 1
(
10
𝑧 − 10
) = 225
tan (tan
− 1
)) = tan 225
10
𝑧− 10
Foi possível achar o valor de z usando um controlador PD, agora vamos aplicar a condição de
magnitude para achar o valor de Kc.
Condição de magnitude
−𝟏𝟎+𝟏𝟎𝒋
100 𝐾𝑐(𝑠+𝑧)
𝑠(𝑠
2
−𝟏𝟎+𝟏𝟎𝒋
= 1 ; vamos substituir o valor de z
100 𝐾𝑐|𝑠+ 20 |
− 10 + 10 𝑗
| 𝑠
|
− 10 + 10 𝑗
×
| 𝑠
2
|
− 10 + 10 𝑗
= 1 ; substituindo o valor de s
100 𝐾𝑐|− 10 + 10 𝑗+ 20 |
| − 10 + 10 𝑗
| ×
| − 100 𝑗
|
100 𝐾𝑐| 10 + 10 𝑗|
|− 10 + 10 𝑗|×|− 100 𝑗|
= 1
100 𝐾𝑐
√ 10
𝟐
+𝟏𝟎
𝟐
√ (− 10 )
2
2
×
√ (− 100 )
2
100 𝐾𝑐× 10 √ 2
10 √ 2 × 100
= 1 → Kc = 1
Com z = 20, temos Kc = 1 e o controlador fica Gc = 1× (𝑠 + 20 ) = 𝑠 + 20
E o Gc×G(s)=
100 (𝑠+ 20 )
𝑆(𝑆
2
; Nessas condições, tendo um feedback unitário, o nosso LGR é:
GC = tf([1 20], [1])
GH = tf([100], [1 10 100 0])
H = feedback (GH*GC, 1)
rlocus (H)
figure (1)
Fig.11. LGR com o controlador antes do ajuste
E a resposta transitória é:
Fig.12. Resposta transitória antes do ajuste
Percebe-se que os polos determinantes encontrados (2.66e- 15 ± 14. 1 ) estão muito distantes dos polos
pretendidos (- 10 ± 10 𝑗). Então, tentamos fazer alguns ajustes para ver se nos aproximamos o máximo
possível dos polos pretendidos.
Alterando o valor de z para z = - 36, aproximamos os polos para - 9.7±17j
GC = tf([1 - 36], [1])
GH = tf([100], [1 10 100 0])
H = feedback (GH*GC, 1)
Como o controlador PID possui três parâmetros: ganho proporcional, ganho integral e ganho
derivativo, ele seria controlador ideal para atender às necessidades do projecto. Mas os cálculos
mostraram que não é possível ter um controlador PID no sistema dado de modo a obter os polos
dominantes pretendidos e, por isso, acabamos por usar um controlador PD.
Usando um controlador PD, torna-se quase impossível achar um ponto em que os valores de 𝜎 e 𝜔
𝑑
,
mas o grupo tentou aproximá-los o máximo possível.
E uma vez que obtivemos todos os polos no semiplano esquerdo de s, diz-se que o sistema é estável.
K. OGATA. Engenharia de Controle Moderno - Segunda Edição. São Paulo – Brasil,
T. Analog and Digital Control System Design, Sunders College Publishing, USA, 1993