Download Exam 2 Solutions - Advanced Structural Analysis - Spring 2011 | CIVL 4440 and more Exams Civil Engineering in PDF only on Docsity!
Name ________________________________
CIVL 4440/6440 Exam No. 2 Spring 2011
**_To ensure that you receive the maximum credit you deserve, please do the following:
- Write legibly
- Show all work
- Provide units on all results
- Box in final results_**
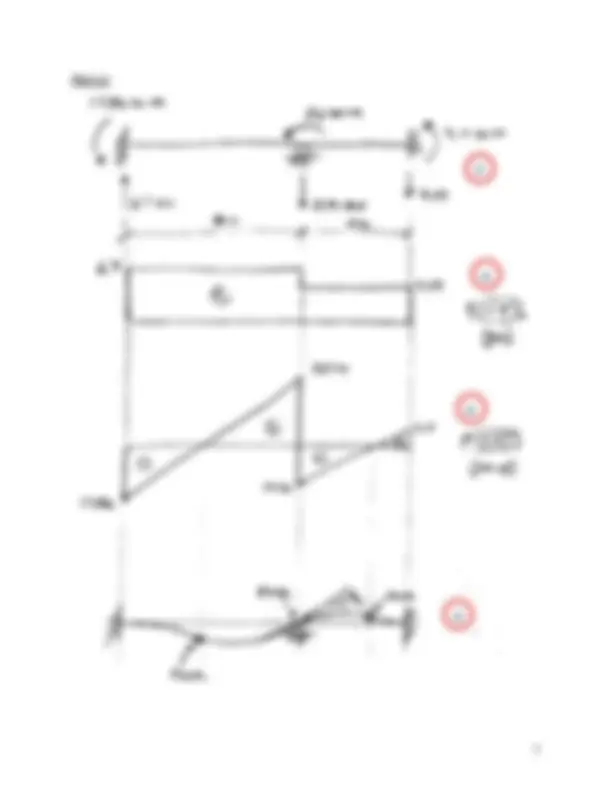
55 points 1) The beam shown below is subjected to a concentrated moment at b and is supported by fixed supports at a and c and a roller support at b. As shown below, the second moment of area about the axis of bending (I) is different for each beam segment. The modulus of elasticity (E) is 200 GPa (200 kN/mm^2 ). The global stiffness matrix for the structure is given below (units are kN for force, mm for length, and radians for rotation) along with the global displacement vector.
I = 200 x 10^6 mm^4 I = 50 x 10 6 mm 4
Pzb = 50 kN-m
7 7
7 7
7
2.0 x 10 3750 1.0 x 10 0 0 1.898 1350 0.96 2400 2.8 x 10 2400 0.4 x 10
. 0.96 2400 0.8 x 10
K
Sym
a a b b c c v
v
v
a) Determine the degree of static indeterminacy.
b) Determine the degree of kinematic indeterminacy.
c) Compute the displacements at the free DOF's.
d) Compute the reactions at the support DOF's.
Solution
e) Draw a free-body diagram of the structure and sketch the internal shear force and bending moment diagrams. For the diagrams, show the positive sign convention and units. Also, using the bending moment diagram carefully sketch the deflected shape. Any points of inflection should be clearly indicated (exact locations do NOT need to be determined).
f) Compute the value of the global stiffness coefficient associated with the 3rd^ row, 3 rd column of the global stiffness matrix. Do this by imposing a unit displacement along the appropriate DOF while holding all other DOF's fixed. Show a sketch of the structure in its deformed position associated with computation of this stiffness coefficient. Verify that your computed value matches that given in the global stiffness matrix.
g) Compute the external work done on the structure by the applied moment. Also, compute the internal strain energy. For both cases, provide the result in units of Joules (J). Recall that 1 Joule = 1 N-m.
Part (c)
P ^ ^ K
7 7
7 7
7
2.0 x 10 3750 1.0 x 10 0 0 1.898 1350 0.96 2400 2.8 x 10 2400 0.4 x 10
. 0.96 2400 0.8 x 10
ya a za a yb b zb b yc c zc c
R v R R v P R Sym v R
Pf^ ^ ^ Kff f
Pzb ^ 2.8 x 10^7 ^ b
7 1 2.8 x 10 50000 0.001786 rad
b ^
Part (d)
Ps^ ^ ^ Ksf f
7 7
7 7
3750 3750 6.70 kN 1.0 x 10 1.0 x 10 17857.1 kN-mm 1350 1350 0.001786 2.41 kN 2400 2400 4.29 kN 0.4 x 10 0.4 x 10 7142.9 kN-mm
^ ^ ^ ^ ^ ^ ^
^ ^ ^
^ ^
^ ^ ^
ya za yb b yc zc
R
R
R
R
R
3
2
2 4
2 4
Part (e)
5
4
6
4
45 points 2) The beam shown below is subjected to a distributed load and a concentrated load and is supported by a fixed support at a and roller supports at b and c. As shown below, the second moment of area about the axis of bending (I) is different for each beam segment. The modulus of elasticity (E) is 200 GPa (200 kN/mm^2 ). The global stiffness matrix for the structure is given below (units are kN for force, mm for length, and radians for rotation) along with the global displacement vector.
I = 400 x 10 6 mm 4 I = 200 x 10^6 mm^4
7 7
7 7
7
3.2 x 10 4800 1.6 x 10 0 0 1.90 1050 0.94 3750 5.2 x 10 3750 1.0 x 10
. 0.94 3750 2.0 x 10
K
Sym
a a b b c c v
v
v
a) Determine the degree of static indeterminacy.
b) Determine the degree of kinematic indeterminacy.
c) Obtain the displacements at the free DOF's.
d) Obtain the reactions at the support DOF's.
e) Compute the value of the global stiffness coefficient associated with the 1st^ row, 4th column of the global stiffness matrix. Do this by imposing a unit displacement along the appropriate DOF while holding all other DOF's fixed. Show a sketch of the structure in its deformed position associated with computation of this stiffness coefficient. Verify that your computed result matches that given in the global stiffness matrix.
Part (a) and (b) The determinacy of a structure is based on the structure itself without consideration of any particular loads acting on the structure. Thus, in the case of a structure composed of general framework elements, we could consider internal forces at the ends of the elements that include three forces (two shear forces acting along the perpendicular cross-sectional axes and an axial force acting along the longitudinal axes) and three moments (bending about two perpendicular cross-sectional axes and twisting about the longitudinal axis). This would result in a 12 x 12 general framework element stiffness matrix for each element and thus, in this case where we have two elements, an 18 x 18 stiffness matrix (since joint b is common to both elements).
For the particular beam in this problem, the stiffness matrix provided has size 6 x 6 (there are 6 DOF's) and relates only vertical forces and moments at the three joints to vertical displacements and rotations at the same joints. Considering only these forces, the structure has 4 reactions (one moment at joint a and three vertical forces at joints a, b, and c) and two equilibrium equations (e.g., sum of the forces in the vertical direction and sum of the moments about any point). Thus, the structure is 2 degrees statically indeterminate. Note that, if the problem were extended to consider axial forces, the size of the stiffness matrix would be 9 x 9 (there would be 9 DOF's) and the number of reactions would increase to 5 and the number of equilibrium equations would increase to 3, resulting in a structure that is 2 degrees statically indeterminate.
As noted above, the 6 x 6 stiffness matrix defines a structure with 6 DOF's. Four of the DOF's are associated with supports and two are associated with free DOF's (rotation at b and c). Thus, the structure is 2 degrees kinematically indeterminate. If the problem were extended to consider axial deformations, the size of the stiffness matrix would be 9 x 9 which defines a structure with 9 DOF's, 5 of which would be associated with supports and 4 of which would be free (rotation and horizontal translation at both b and c). Thus, the structure would be 4 degrees kinematically indeterminate.
Summary: For the given stiffness matrix, the structure is:
2 degrees statically indeterminate
2 degrees kinematically indeterminate
If the problem were extended to consider axial forces and deformations, the structure would be:
2 degrees statically indeterminate
4 degrees kinematically indeterminate
2
2
7 7 7 7
(^0) 5.2 x 10 1.0 x 10 1670 (^0) 1.0 x 10 2.0 x 10 40000
^
^
b c
7 7 7 7
1670 5.2 x 10 1.0 x 10 40000 1.0 x 10 2.0 x 10
^ ^ ^
b c
7 7 1 4 7 7 3
5.2 x 10 1.0 x 10 1670 3.9 x 10 rad 1.0 x 10 2.0 x 10 40000 2.2 x 10
(^)
^ ^ ^
^
b c
If needed, the matrix inverse can be calculated by hand as follows:
7 7 1 7 7 7 7 7 7 7 7 7 7
5.2 x 10 1.0 x 10 1 2.0 x 10 1.0 x 10 1.0 x 10 2.0 x 10 5.2 x 10 2.0 x 10 1.0 x 10 1.0 x 10 1.0 x 10 5.2 x 10
(^)
8 8 8 8
2.13 x 10 1.06 x 10 1.06 x 10 5.53 x 10
Alternatively, could write out the two equations and then solve it as two equations in two unknowns:
7 7
7 7
1670 5.2 x 10 1.0 x 10
40000 1.0 x 10 2.0 x 10
b c
b c
7 7
1670 1.0 x 10 5.2 x 10
c b
7 7 7 7
1670 1.0 x 10 40000 1.0 x 10 2.0 x 10 5.2 x 10
c c
3 4
2.2 x 10 rad 3.9 x 10 rad
c b
4
Part (d)
Ps^ ^ ^ K^ sf ^ f PsF
7
1.6 x 10 0 41670 1050 3750 45 3750 3750 20
^
^
^ ^ ^
^
^ ^ ^ ^
ya za (^) b yb (^) c yc
R
R
R
R
(^7 ) 3
4800 0 25 23.1 kN 1.6 x 10 (^0) 3.9 x 10 41670 35430 kN-mm (^1050 3750) 2.2 x 10 45 53.6 kN 3750 3750 20 13.2 kN
^ ^ ^
^
Part (e)
2 6 4 (^14 )
6 6 200 kN/mm^ 400 x 10^ mm 4800 kN/rad 10000 mm
EI K L
From global stiffness matrix:
K 14 4800 kN/rad
2
4
1
2 4 2
2
Equations which may be useful
^ ^ ^ ^ (^) ^ ^ ^ ^ ^ ^ (^)
F f ff^ fs f f F s (^) sf ss s s
P K^ K P
P (^) K K P
^ ^ ^ ^ ^ ^ ^ ^ ^
F P f K (^) ff f K (^) fs s Pf
^ ^ ^ ^ ^
F Ps K (^) sf f K (^) ss s Ps
^ '
T k k (^) F ' F (^) '
1 2
T W Pf f
^
T
U f Kff f
If
^
^
a b d b d b A A c d A c a ad bc c a
1 1
1 1
(^) ^ (^)
T
T
d d k d d
Fs^ Ff
